CW-ERM: Improving Autonomous Driving Planning with Closed-loop Weighted Empirical Risk Minimization
Improving Autonomous Driving Planning with Closed-loop Weighted Empirical Risk Minimization
Introduction
Imitation Learning (IL), and especially Behavioral Cloning (BC) are widely used today for many tasks. BC is of especial interest because it can take advantage of the supervised learning properties such as sample complexity and learning from historical data (demonstrations). Behavioral Cloning (BC), however, still face fundamental challenges
One of the main issues of BC that is often overlooked, especially in policies trained for autonomous vehicles (AVs) is the mismatch between the training and inference-time distributions. Usually, BC policies are trained in an open-loop fashion, predicting the next action given the immediate previous action and optionally conditioned on recent past actions. This is quite different than the way that these policies are evaluated and deployed. During test time, the policy is used not only to predict an action, but this action is also execute in the simulated or real-world environment and impacts the next state. This difference is explained in the image below:

When executed in real-world (or even in a simulated environment), small predictions errors can drive covariate shift and make the network predict in an out-of-distribution regime. In the animation below we can see an example of a policy that starts to diverge and is unable to recover:

If we imagine a State-Action manifold (SxA) like in the figure below, we can see how the state-action datapoints start to diverge from the data that the model was trained on:
In this work, we address the mismatch between training and inference mentioned above through the development of a simple training principle. Using a closed-loop simulator, we first identify and then reweight samples that are important for the closed-loop performance of the policy. We call this approach CW-ERM (Closed-loop Weighted Empirical Risk Minimization), since we use Weighted ERM
- We motivate and propose Closed-loop Weighted Empirical Risk Minimization (CW-ERM), a technique that leverages closed-loop evaluation metrics acquired from policy rollouts in a simulator to debias the policy network and reduce the distributional differences between training (open-loop) and inference time (closed-loop);
- We evaluate CW-ERM experimentally on a challenging urban driving dataset in a closed-loop fashion to show that our method, although simple to implement, yields significant improvements in closed-loop performance without requiring complex and computationally expensive closed-loop training methods;
- We also show an important connection of our method to a family of methods that addresses covariate shift through density ratio estimation.
Closed-loop Weighted Empirical Risk Minimization (CW-ERM)
Problem setup
The traditional formulation of supervised learning for imitation learning, also called behavioral cloning (BC), can be formulated as finding the policy \(\hat{\pi}_{BC}\):
\[\DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \begin{align} \label{eqn:bc-erm} \hat{\pi}_{BC} = \argmin_{\pi \in \Pi} \mathbb{E}_{s \sim d_{\pi^*}, a \sim \pi^*(s)}[\ell(s,a,\pi)] \end{align}\]where the state $s$ is sampled from the expert state distribution \(d_{\pi^*}\) induced when following the expert policy \(\pi^*\). Actions $a$ are sampled from the expert policy \(\pi^*(s)\). The loss \(\ell\) is also known as the surrogate loss that will find the policy \(\hat{\pi}_{BC}\) that best mimics the unknown expert policy \(\pi^*(s)\). In practice, we only observe a finite set of state-action pairs \({(s_i, a^*_i)}_{i=1}^m\), so the optimization is only approximate and we then follow the Empirical Risk Minimization (ERM) principle to find the policy \(\pi\) from the policy class \(\Pi\).
If we let \(\mathbb{E}_{s \sim d_{\pi^*}, a \sim \pi^*(s)}[\ell(s,a,\pi)] = \epsilon\), then it follows that \(J(\pi) \leq J(\pi^*) + T^2 \epsilon\) as shown by the proof in
When the policy \(\hat{\pi}_{BC}\) is deployed in the real-world, it will eventually make mistakes and then induce a state distribution \(d_{\hat{\pi}_{BC}}\) different than the one it was trained on ( \(d_{\pi^*}\)). During closed-loop evaluation of driving policies, non-imitative metrics such as collisions and comfort are also evaluated. However, they are often ignored in the surrogate loss or only implicitly learned by imitating the expert due to the difficulty of overcoming differentiability requirements, as smooth approximations of these metrics are still different than the non-differentiable counterparts often used. These policies can often show good results in open-loop training, but perform poorly in closed-loop evaluation or when deployed in a real SDV due to the differences between \(d_{\hat{\pi}_{BC}}\) and \(d_{\pi^*}\), where the estimator is no longer consistent.
CW-ERM
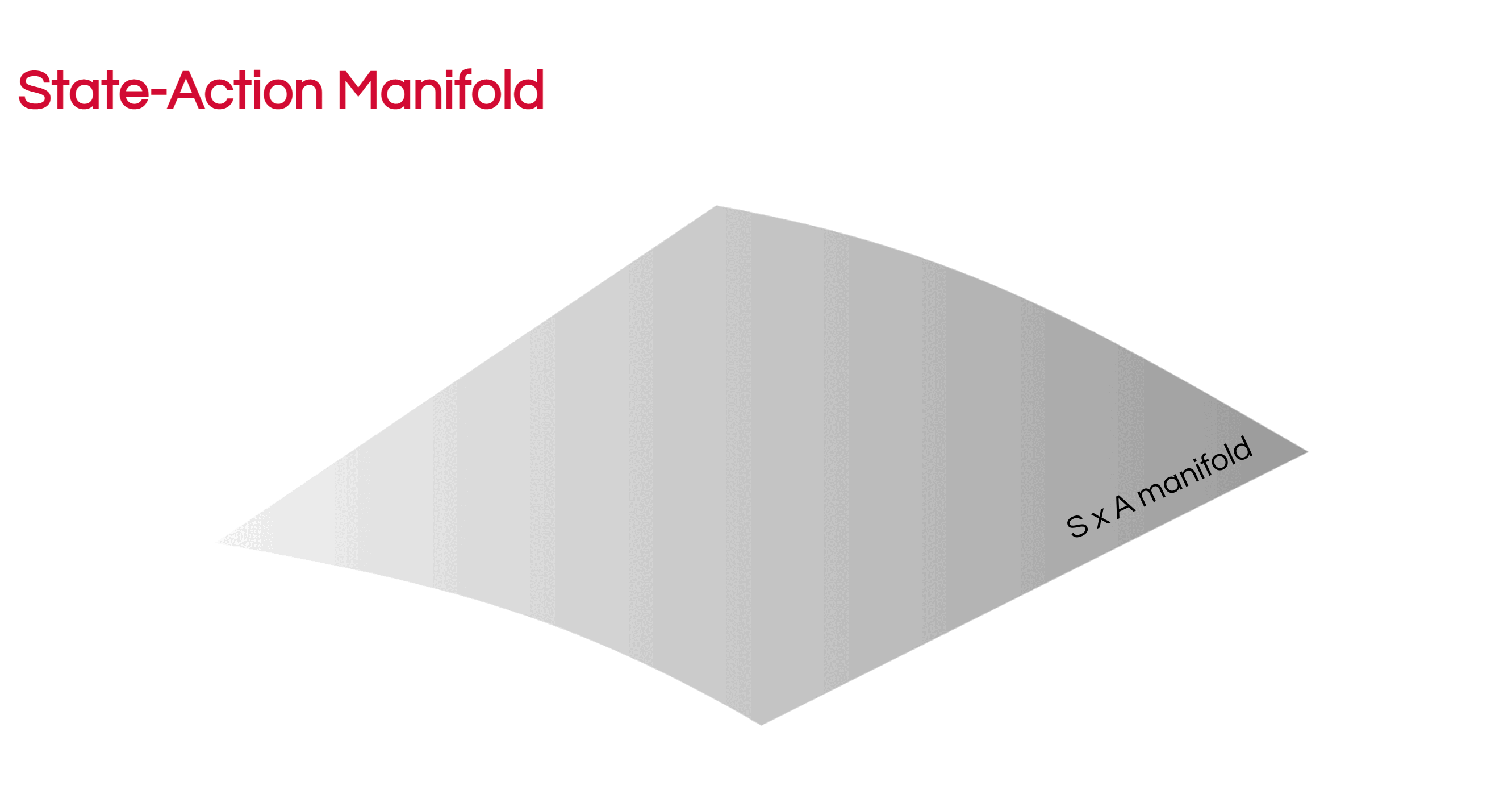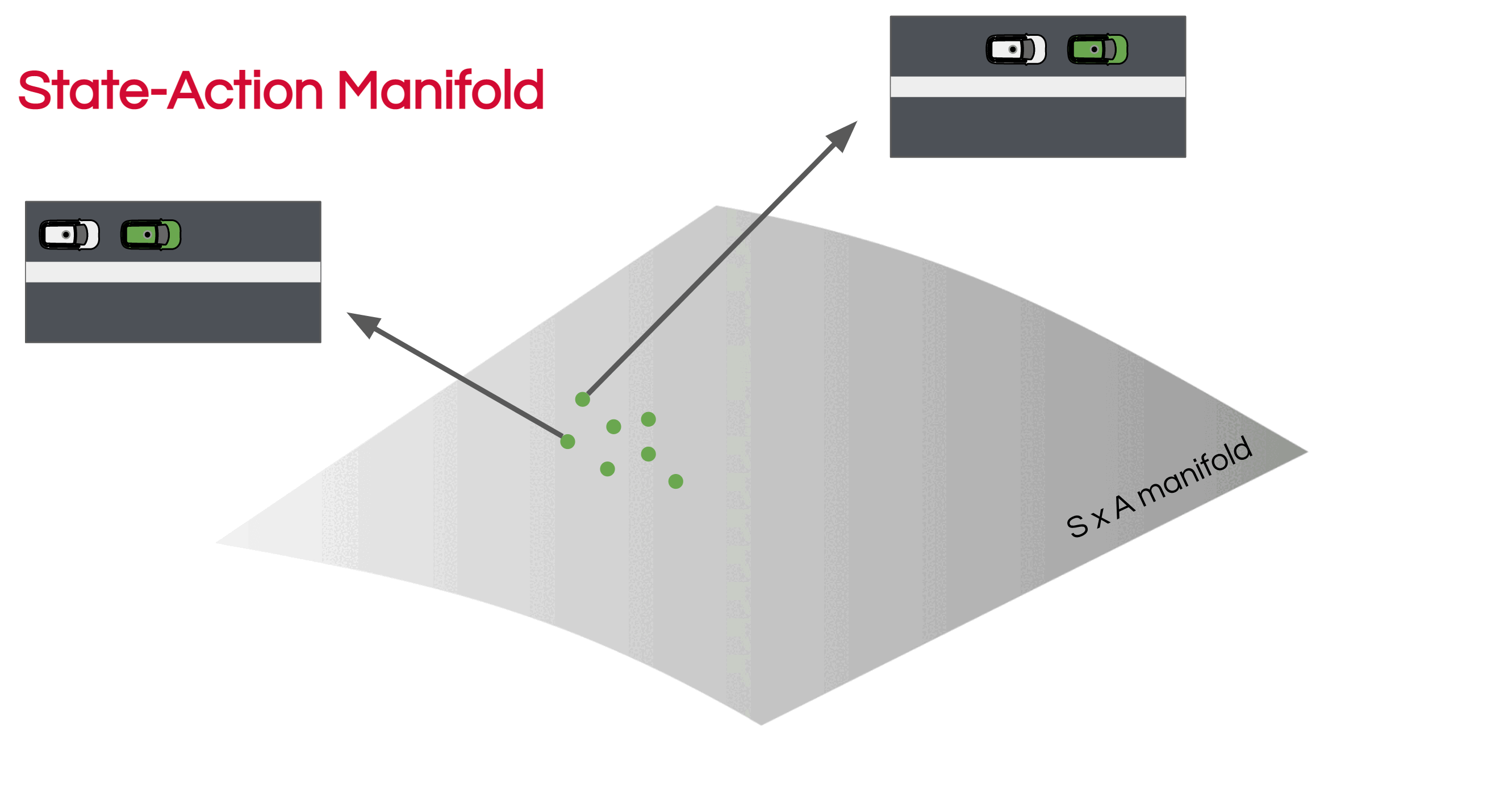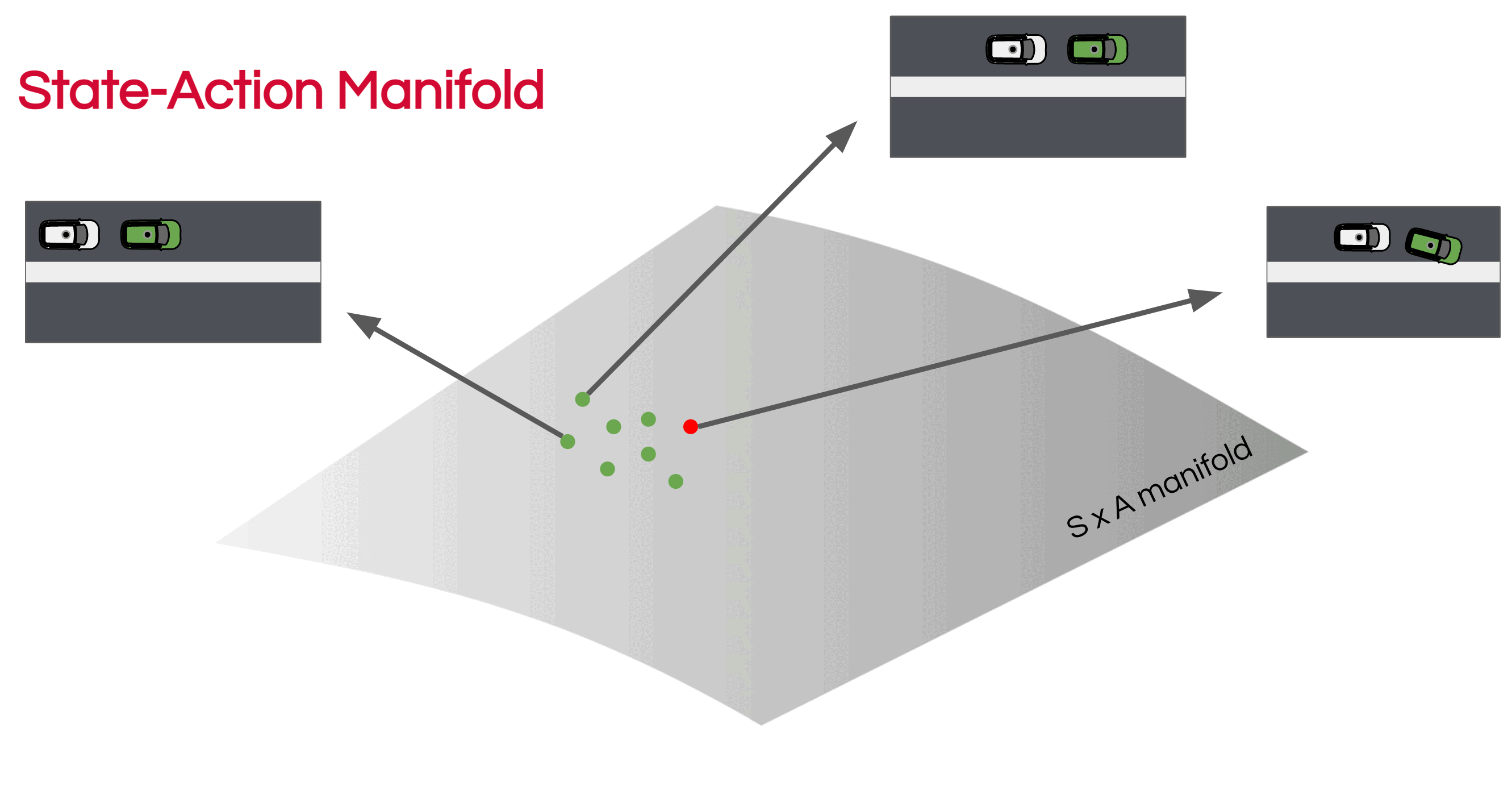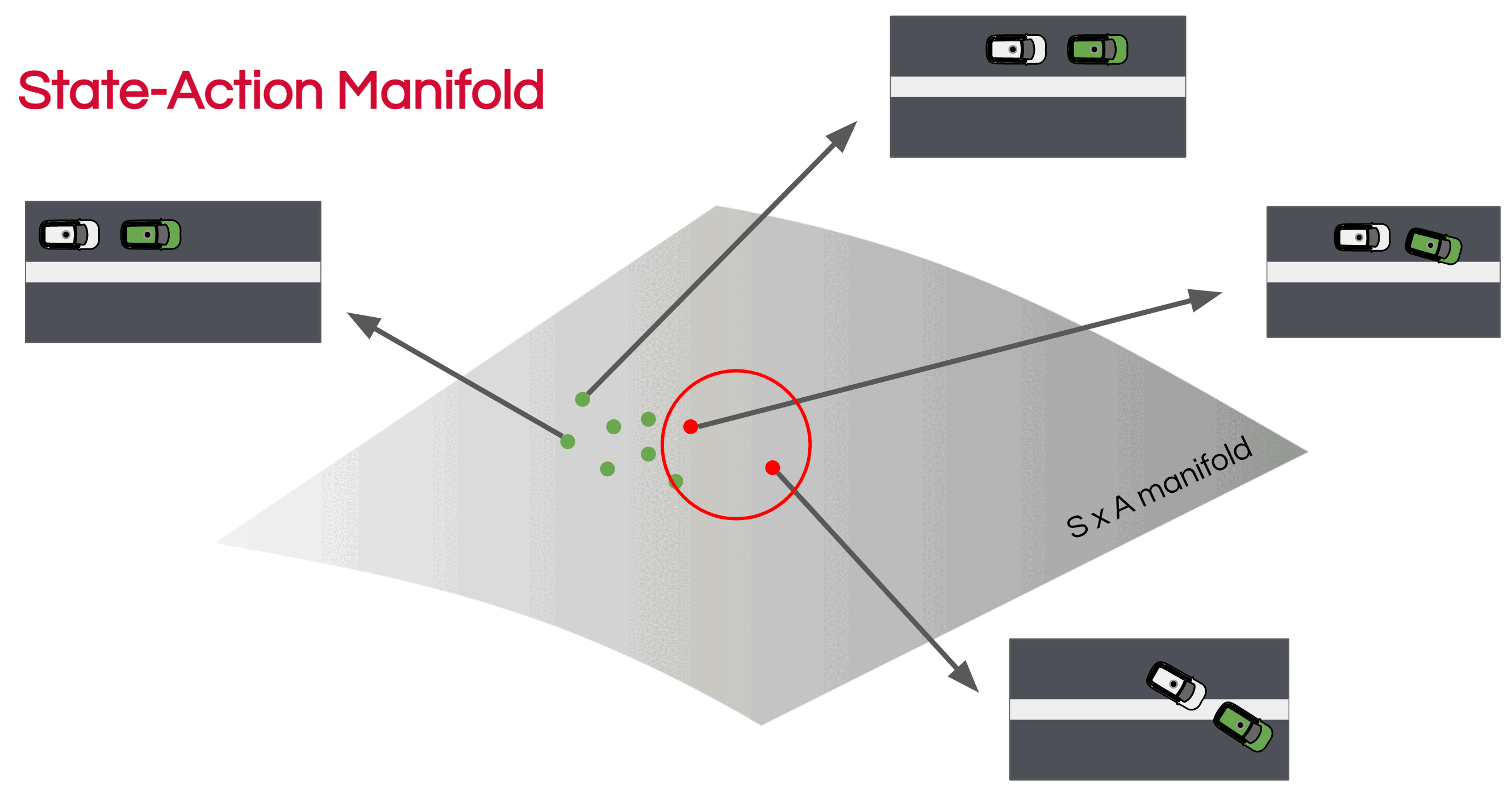
In our method, called Closed-loop Weighted Empirical Risk Minimization (CW-ERM), we seek to debias a policy network from the open-loop performance towards closed-loop performance, making the model rely on features that are robust to closed-loop evaluation. Our method consists of three stages: the training of an identification policy, the use of that policy in closed-loop simulation to identify samples, and the training of a final policy network on a reweighted data distribution. More explicitly:
Stage 1 (identification policy)
Train a traditional BC policy network in open-loop using ERM, to yield \(\hat{\pi}_{\text{ERM}}\).
Stage 2 (closed-loop simulation)
Perform rollouts of the \(\hat{\pi}_{\text{ERM}}\) policy in a closed-loop simulator, collect closed-loop metrics and then identify the error set below:
\[\begin{align} \label{eqn:error-set} E_{\hat{\pi}_{\text{ERM}}} = \{(s_i, a_i)~\text{s.t.}~ {C(s_i, a_i)} > 0 \}, \end{align}\]where \(\text{s}_i\) is a training data sample, or scene with a fixed number of timesteps from the training set, \(\text{a}_i\) is the action performed during the roll-out and \(C(\cdot)\) is a cost such as the number of collisions found during closed-loop rollouts.
Stage 3 (final policy)
Train a new policy using weighted ERM where the scenes belonging to the error set \(E_{\hat{\pi}_{\text{ERM}}}\) are upweighted by a factor \(w(\cdot)\), yielding the policy \(\hat{\pi}_{\text{CW-ERM}}\):
\[\begin{equation} \label{eqn:bc-cw-erm} \argmin_{\pi \in \Pi} \mathbb{E}_{s \sim d_{\pi^*}, a \sim \pi^*(s)}[w(E_{\hat{\pi}_{\text{ERM}}}, s) \ell(s,a,\pi)] \end{equation}\]As we can see, the CW-ERM policy in Equation \(\ref{eqn:bc-cw-erm}\) is very similar to the original BC policy trained with ERM in Equation \(\ref{eqn:bc-erm}\), with the key difference of a weighting term based on the error set from closed-loop simulation in Stage 2. In practice, although statistically equivalent, we upsample scenes by a fixed factor rather than reweighting, as it is known to be more stable and robust
By training a policy using CW-ERM, we expect it to upsample scenes that perform poorly in closed-loop evaluation, making the policy network robust to the covariate shift seen during inference time while unrolling the policy. In the figure below you can see a visual overview of the steps involved into CW-ERM:

Interesting connection with covariate shift adaptation with density ratio estimation
One important connection of our method is with covariate shift correction using density ratio estimation
where \(r(s)\) is defined as the density ratio between test and training distributions:
\[\begin{equation} \label{eqn:density-ratio} r(s) = \frac{p_{\text{test}}(s)}{p_{\text{train}}(s)} \end{equation}\]In practice, \(r(s)\) is difficult to compute and is thus estimated. The density ratio will be higher when the sample is more important for the test distribution. In our method (CW-ERM), instead of using the density ratio to weight training samples, we resample the training set based on an estimate of each data point’s importance towards good closed-loop behaviours. Like the density ratio, the weighting in our case will also be higher for when the sample is important for the test distribution.
One key characteristic of the importance weighted estimator is that it can be consistent even under covariate shift. We leave, however, the analysis of theoretical properties of our approximation for future work.
Experimental evaluation
Network architecture
Our method is agnostic to model architecture choices. To evaluate our CW-ERM approach, we adopt the recent network architecture of
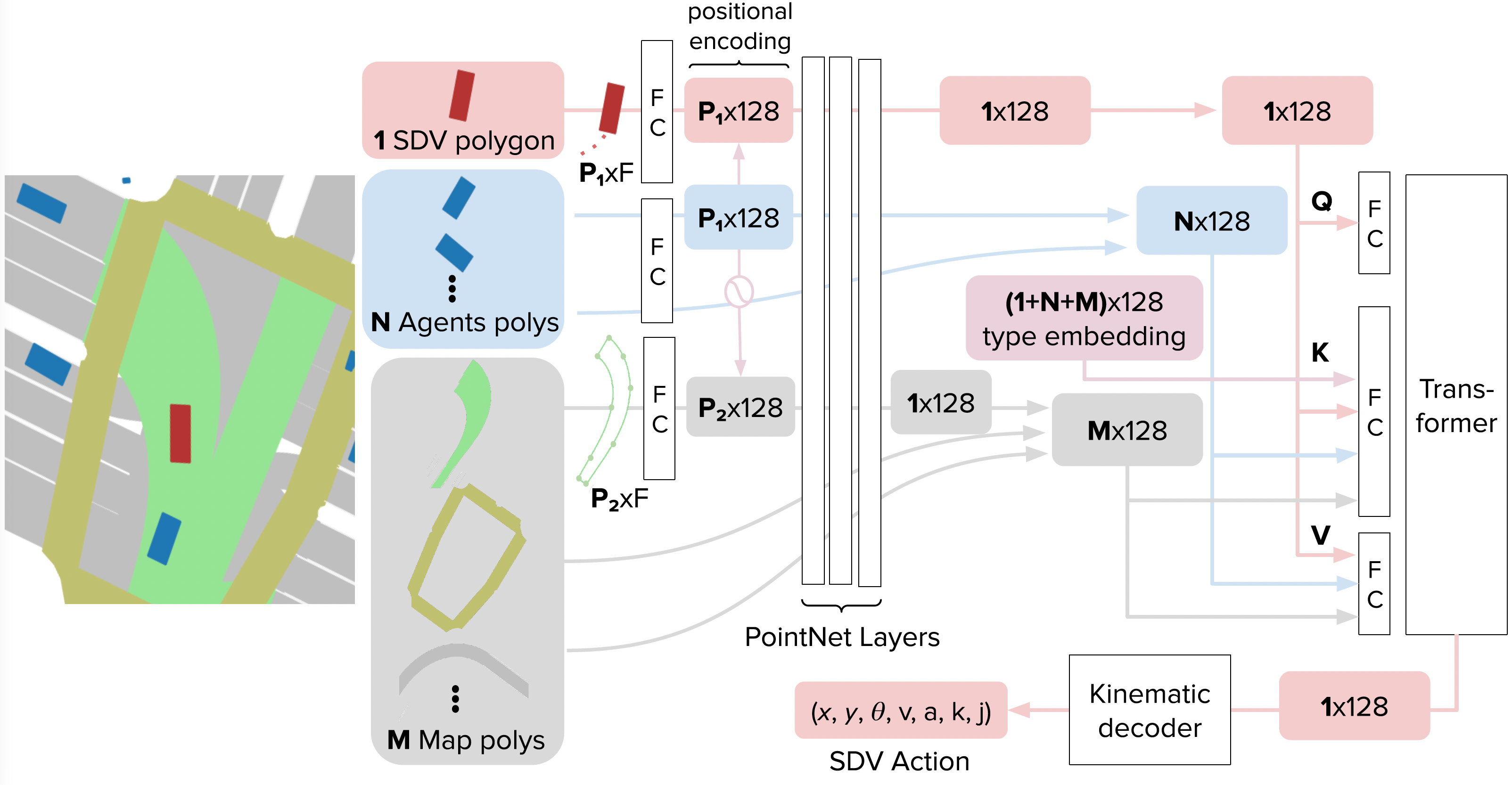
Evaluation framework
We compute the closed-loop evaluation metrics by doing rollouts of the policy in the log-replayed scenes on a simulator (please refer to the reproducibility section for details on the open-sourcing of the simulator and metrics used in this work). During the unroll, trajectories are recorded. An evaluation plan composed of a set of metrics and constraints is executed over the recorded trajectories. We count every scene that violated a constraint (e.g., a collision) and then compute the confidence intervals (CIs) for each metric using a Binomial exact posterior estimation with a flat prior, which gives similar results (up to rounding errors) to bootstrapping as recommended in
Metrics computed in the closed-loop simulator are used to construct the error set. In our evaluation we consider certain important metrics: the number of front collisions, side collisions, rear collisions, and distance from reference trajectory. The distance from reference trajectory considers the entire target trajectory for the current simulated point. A failed scene with respect to this metric is one where the distance of the simulated center of the SDV to the closest point in the target trajectory is farther than four meters.
In our evaluation, we perform two sets of experiments: single metric and multi metric. In single metric experiments we construct the error set using only a single metric, while for multi metric we use scenes from multiple metrics together.
Results
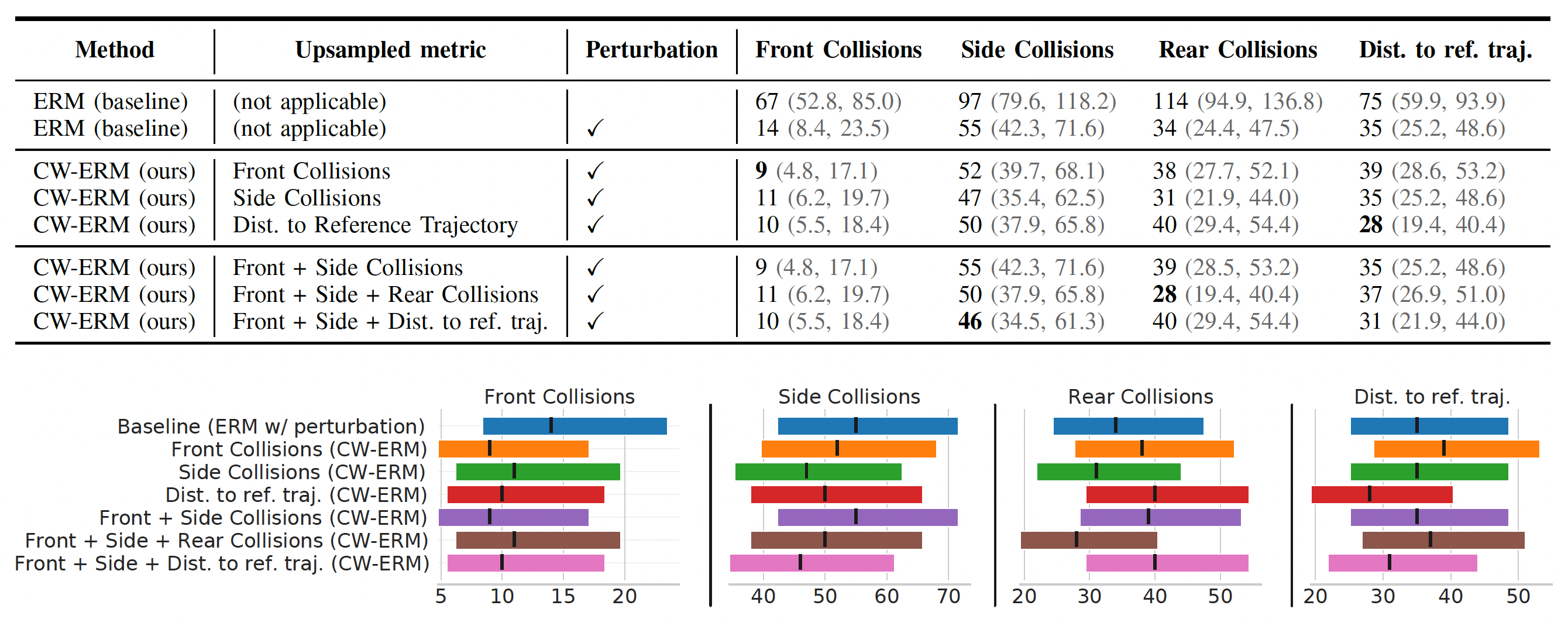
In the table below we show a baseline method of behavioral cloning (ERM) with and without perturbations together with the results from single and multi-metric experiments. Lower is better for all metrics:
Single-metric
We show the results from single metric experiments in Figure 6. We can see that the number of collisions significantly reduced for both side and front collision experiments. We found improvements in the range of ~35% on the test set for some metrics when compared to the baseline.
We also found that the largest margin of improvements targeting single metrics in isolation were seen when using single metric based error set, while a balance was achieved when targeting multiple metrics, which suggests a Pareto front of solutions when targeting multiple objectives.
Variance is also lower in some cases when compared to the baseline. We note that while upsampling a certain metric, it shows noticeable improvements in other related metrics. For example, in our single metric experiments, we see that improving side collisions also improve rear collisions. This is evidence that the model is not only getting better at side collisions but also becoming less passive (as indicated by reduction in rear collisions, due to log-replayed agents in simulation that are non-reactive).
Multi-metric
In our multi-metric experiments, we combine two or more metrics - namely \(m_{1},m_{2}..m_{N}\) - into a single upsampling experiment. The metrics are equally weighted and hence scenes that fail due to any \(m_i\) will be added to the error set. While improvements are noticeable upon combining Front and Side collisions or Front, Side and Distance to the reference trajectory in Figure 6, considerable regression is observed when adding rear collisions. As we can see from the experiments, this is clearly related to the amount of false-positives (FPs) in rear collisions due to the lack of agent reactivity during log playback in the simulator.
Closed-loop evaluation samples
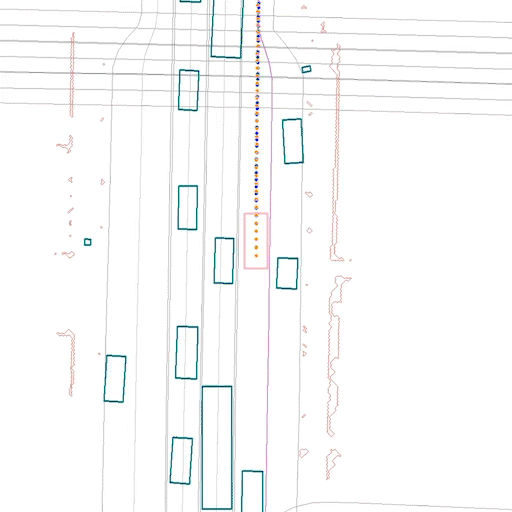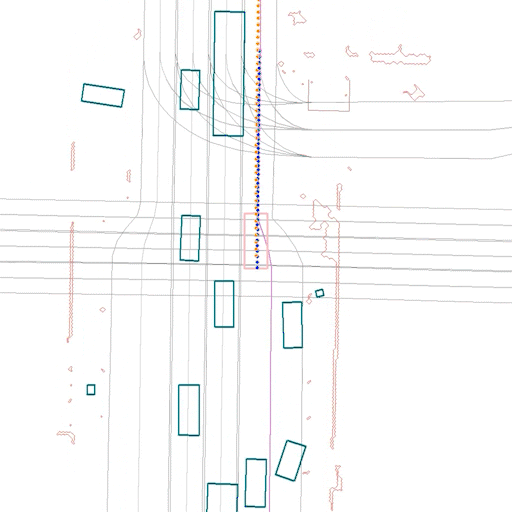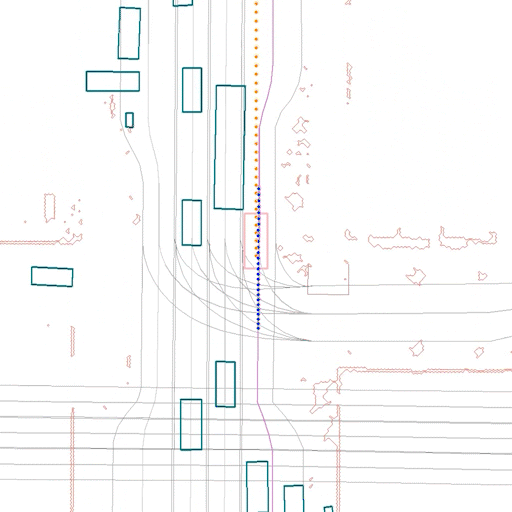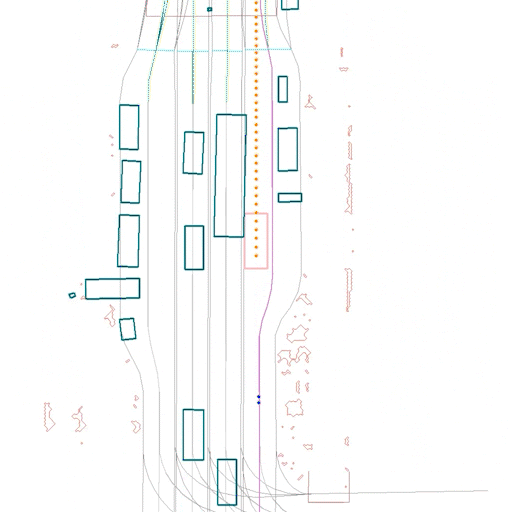
Here we show some samples from our test set, comparing the same scene using ERM (left) and CW-ERM (right), in this case we can see CW-ERM avoiding a front collisions when compared to the traditional ERM policy:


In the scene below, also from the test set, we can see CW-ERM avoiding a side collision when compared to a traditional ERM policy:
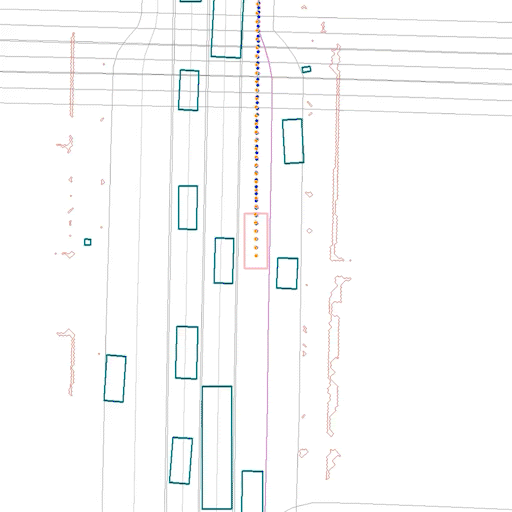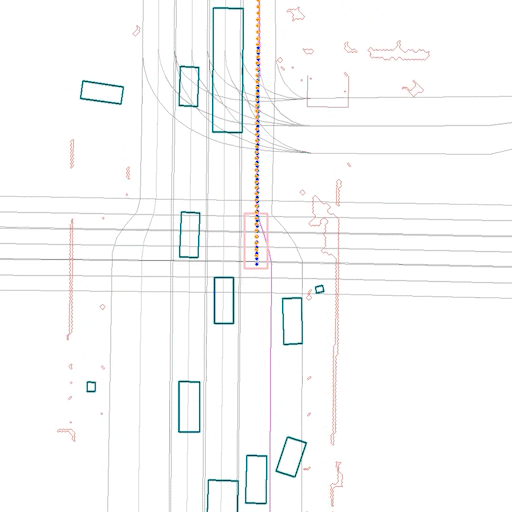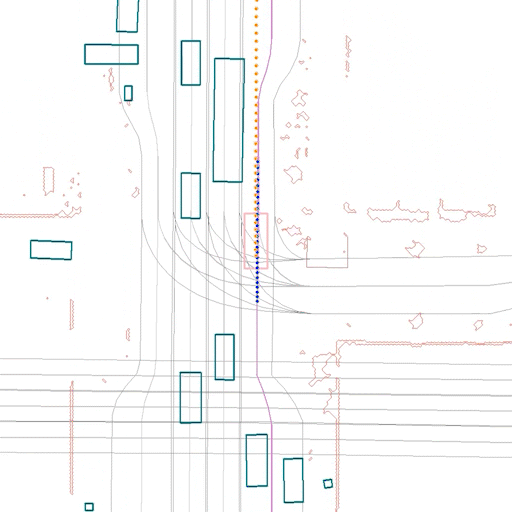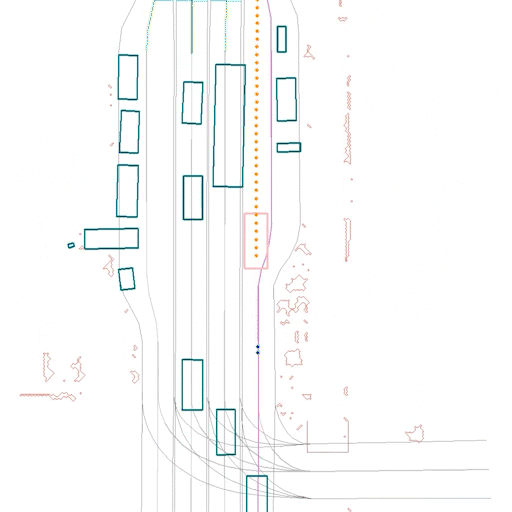
Discussion
Most recent improvements in imitation learning are based on improving the asymptotic performance of algorithms. In this work we showed a different direction that tackles the problem by directly addressing the mismatch between training and inference without requiring an extra human oracle or adding extra complexity during training. Our method is as simple as upsampling scenes by leveraging any existing simulator and training two models, yet it showed that there is still room for significant improvements without having to deal with human-in-the-loop, training rollouts or impacting the policy inference latency. We also described an important potential connection of our method with density ratio estimation for covariate shift correction
Citation
If you found our work useful, please consider citing it:
@article{kumar2022-cwerm,
doi = {10.48550/ARXIV.2210.02174},
url = {https://arxiv.org/abs/2210.02174},
author = {Kumar, Eesha and Zhang, Yiming and Pini, Stefano and Stent, Simon and Ferreira, Ana and Zagoruyko, Sergey and Perone, Christian S.},
title = {CW-ERM: Improving Autonomous Driving Planning with Closed-loop Weighted Empirical Risk Minimization},
publisher = {arXiv},
year = {2022},
}
Acknowledgement
We would like to thank Kenta Miyahara, Nobuhiro Ogawa and Ezequiel Castellano for the review of this work and everyone from the UK Research Team and the ML Planning team who supported this work through the ecosystem needed for all experiments, and for the fruitful discussions.
Reproducibility
We make available our closed-loop simulator and the closed-loop metrics used in this work in the L5Kit open-source repository.